Tips:
- Turn on the gas just before lighting your match;
- Turn off the gas to extinguish the flame;
- Ensure tubing is not going to catch on fire, ideally, tape it down.

Tips:
There are two types of filtration used in CHEM 103. Follow the links to learn more about filtration techniques:
Spectrophotometers contain a white light source, a diffraction grating, and a slit to select a specific wavelength. The selected wavelength of light passes through a sample, and any light that is absorbed is quantified as the absorbance. The absorbance range is 0 (no light absorbed) to 1 or more (lots of light absorbed). According to Beer’s law, absorbance and concentration are directionally proportional: samples with a high concentration of light absorbing particles have a high absorbance, and those with a low concentration of light absorbing particles have a low absorbance. In principle, any difference in absorbance can be measured with the spectrophotometer, but in practice, it is impossible to tell the difference between two samples if they are (1) too optically dense, meaning basically no light gets through, (2) too dilute, meaning practically all of the light gets through, giving both samples an absorbance of nearly 0, or (3) too similar, meaning there are not enough significant figures.
In everyday life, you have probably noticed that color is often indicative of chemistry. For example, fruit often changes color when it ripens: a green banana contains complex starches (yuck), but a yellow banana contains simple sugars (yum). Color intensity is also indicative of chemistry, particularly in solutions. Today, you will use a spectrophotometer to quantify color hue and intensity for a relatively simple solution of Kool-Aid. This will allow you to derive the relationship between Kool-Aid concentration and color intensity, known as the Beer’s Law.
Spectrophotometers contain a white light source, a diffraction grating, and a slit to select a specific wavelength. The selected wavelength of light passes through a sample, and any light that is absorbed is quantified as the absorbance. The absorbance range is 0 (no light absorbed) to 1 or more (lots of light absorbed). According to Beer’s law, absorbance and concentration are directionally proportional: samples with a high concentration of light absorbing particles have a high absorbance, and those with a low concentration of light absorbing particles have a low absorbance. In principle, any difference in absorbance can be measured with the spectrophotometer, but in practice, it is impossible to tell the difference between two samples if they are (1) too optically dense, meaning basically no light gets through, (2) too dilute, meaning practically all of the light gets through, giving both samples an absorbance of nearly 0, or (3) too similar, meaning there are not enough significant figures. This is analogous to a graduated cylinder, which cannot measure above the highest graduation line or below the lowest graduation line, and cannot differentiate between volumes that are within the uncertainty of the measurement.
Fill out this worksheet. Graph may be submitted on Canvas or printed and attached to the worksheet.
Written by S. Sontum, D. Copeland, and K. Jewett. Edited by R. Sandwick, M. J. Simpson, and R. Bunt
In the summer of 1803 John Dalton was working on the relative weights of elements that combine in chemical reactions. He summarized the results of these experiments in his law of multiple proportions: When two or more elements unite to form more than one compound, the masses of one element that combine with a given mass of another are in ratios of small integers.
For example consider the oxides of nitrogen with the formulas N2O (nitrous oxide or laughing gas), NO (nitric oxide) and NO2 (nitrogen dioxide). Because these compounds contain the same element in different proportions they may be used to illustrate the law of multiple proportions. If we use 14 g of nitrogen to make each of these oxides, the mass of oxygen combining with this mass of nitrogen are 8 g in N2O, 16 g in NO, and 32 g in NO2. These numbers 8: 16: 32 are simple fractions of each other, as required by the law.
To explain these experiments Dalton drew up the tenets of his atomic theory. Is the concept of the atom just a theoretical construct? The atom was not an abstraction to him or to the modern day chemist. Each indivisible atom has a unique physical weight. The multiple proportion ratios are simply a reflection of the mole ratios or atom ratios given by the molecular formula. There has been debate among historians as to the order of Dalton’s two great generalizations. Which came first, the atomic theory or the law of multiple proportions? Most probably in Dalton’s mind the two ideas were essentially one, just as these two ideas are now combined in the modern day concept of a molecular formula.
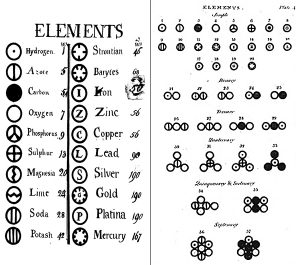
Dalton’s elements http://thehistoryoftheatom.weebly.com/john-dalton.html
In this experiment you will determine the molecular formula of a metal bromide by first decomposing it with heat, then converting it to a metal oxide by oxidation, and finally reducing it to a pure metal. Similar steps are used by the mining industry to refine metals. Metals are often found in nature as metal oxide ores. Metal oxides are examples of inorganic salts [Mn+ O2-] where the metal is found as a positive ion ionically bonded to oxygen dianions (oxides). Formerly, the term oxidation meant “reaction with oxygen” and the term reduction meant “to refine a metal.” Oxidation is now more generally defined as the loss of electrons and reduction is defined as the gain of electrons. Using this definition M2+ is an example of a oxidized metal because it has lost electrons (two) relative to its neutral or elemental form of the metal. A few metal oxides, such as those of silver and mercury, can be decomposed to free metal by heat alone. All others must react with reducing agents. Reduction results in the removal of oxygen as the positive metal is converted to its neutral or metallic form by gaining electrons. In the preparation of metals from their oxide ores, carbon in the form of coke is often used to reduce the metal because it is relatively inexpensive. In the laboratory, hydrogen gas is a very convenient reducing agent. At high temperature hydrogen will reduce many metal oxides including copper oxides.
Hydrogen can easily be generated by the oxidation/reduction reaction between zinc metal and sulfuric acid:
Zn(s) + H2SO4(aq) —> ZnSO4(aq) + H2(g)
You will be given a compound (compound I) that contains only copper and bromine. When heated, compound 1 loses part of its bromine to form a different compound (compound II), liberating bromine gas in the process:
2 CuBrx(s) → 2 CuBry(s) + (x-y) Br2(g)
On subsequent treatment with nitric acid all of the residual bromine is removed in a series of oxidation reactions and only an oxide of copper remains. This series of reactions can be summarized as:
2 CuBry(s) + z O2(g) → 2 CuOz(s) + y Br2(g)
Finally we can determine the mass of copper by reducing the copper oxide to pure metallic copper with hydrogen gas:
CuOz(s) + z H2(g) → Cu(s) + z H2O(g)
From the mass losses accompanying the stepwise removal of bromine, we can calculate how much bromine there was in compound I and compound II. The relationship between these masses and the mass of copper in the sample will allow us to demonstrate the law of multiple proportions.
Note: Perform this lab with a partner.
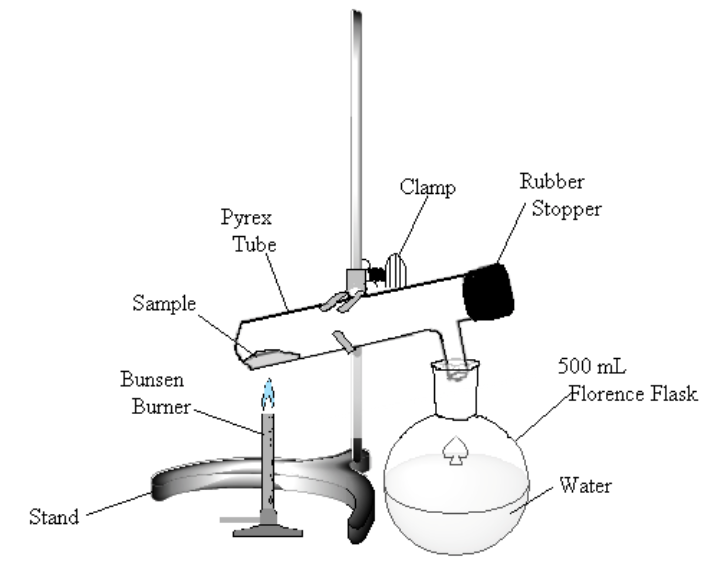
Figure 1
Heat the sample gently. If bromine (a dark-red liquid) condenses at the upper end of the test tube, warm it gently to vaporize the liquid. Continue to heat the sample until no more bromine vapor is evolved (bromine vapor is yellow), perhaps 10 minutes.
Assemble the apparatus shown in Figure 2. Note: be very careful to use the following method for introducing glass connections into rubber stoppers or rubber connectors (very severe cuts can result if the glass tubing breaks and the jagged ends get pushed into the hands): moisten the stopper and tube with a small amount of water or glycerol for lubrication. Grasp stopper and tube close together with a cloth, and insert the tube into the stopper with a twisting motion, being careful and applying pressure gently.
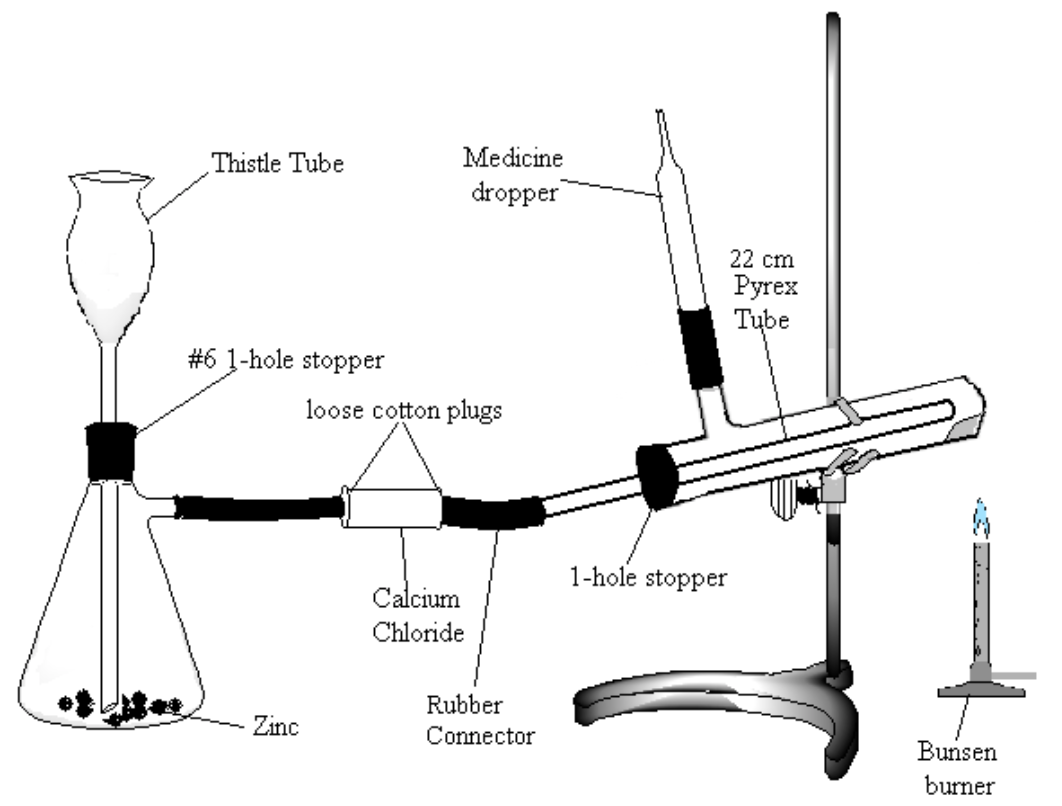
Figure 2
Fill out this worksheet. Turn in either a paper or digital copy.

Dmitri Mendeleev
When Dmitri Mendeleev published the first periodic table, he arranged the elements to illustrate their periodic trends. Many elements that we know of today had not been discovered yet (Note: scientists continue to discover new elements today), so Mendeleev left gaps where there seemed to be discontinuities in the trends. One of these gaps was an element that seemed to be missing from group 14 between silicon and tin. He called the missing element “eka-silicon.”
Clemens Winkler discovered a new element in 1886. Its physical properties were similar to antimony and arsenic, but its chemical reactivity fit with elements in group 14, so it wasn’t clear where the new element fit on the periodic table. Finally, Winkler determined the atomic mass of the new element, which matched Mendeleev’s prediction for eka-silicon, so the element was placed in group 14 and named “Germanium” after his homeland of Germany.
In this experiment, you will measure the density of 3 of the elements in group 14 and predict the density of Germanium.
Density is defined as mass per volume. It is normally expressed in units of g/cm3 or g/mL (these are equivalent). Therefore, to measure the density of these elements, you will need to measure both the mass and the volume.
Measuring the mass is easy: we have highly accurate analytical balances. They are calibrated on a regular basis. Measuring the volume is a little trickier and requires careful attention to significant figures.
Note: this lab is performed individually, but you will need to collaborate with two other students to complete the data analysis. Each student in your group of three will measure the density of one of the elements provided, and you will combine your results to predict the density of germanium. You may need to provide data for more than one group, depending on how many students are in your lab section.
Fill out this worksheet. Turn in either a paper or digital copy. Attach your graphs.
(Hint: If you read through these instructions before coming to lab, plan on completing this step before the pre-lab discussion to ensure the most vibrant colors possible.)

The sun emits a continuous spectrum of ultraviolet (UV), visible, and infrared light. Of particular concern is UV light, which the World Health Organization classifies ultraviolet (UV) light as a known carcinogen. This means that UV light causes cancer. UV light also causes erythema, commonly known as a sunburn, and damages skin fibers, evidenced by wrinkled and sagging skin. 
The Food and Drug Administration (FDA) regulates sunscreen products claiming to protect skin from the sun and assigns a numerical sun protection factor (SPF). The FDA currently requires in vivo testing to measure the SPF; this involves application of the sunscreen to a patch of a volunteer’s skin and then exposing the volunteer to a controlled UV light source until the skin develops a sunburn. The SPF is calculated by comparing the amount of time it takes to sunburn the skin with the sunscreen to the amount of time it takes to sunburn the skin without sunscreen. SPF 15 means it takes 15 times longer to burn the skin with sunscreen than the skin without sunscreen. Unfortunately, this testing requires that a human volunteer gets a sunburn, which increases their risk of skin cancer. The goal of this lab is to develop a laboratory-based scale to measure the SPF without harming human volunteers. Instead of measuring how well a sunscreen protects against sunburn in a human volunteer, you will measure how well a sunscreen blocks UV light in the laboratory using spectrophotometry.
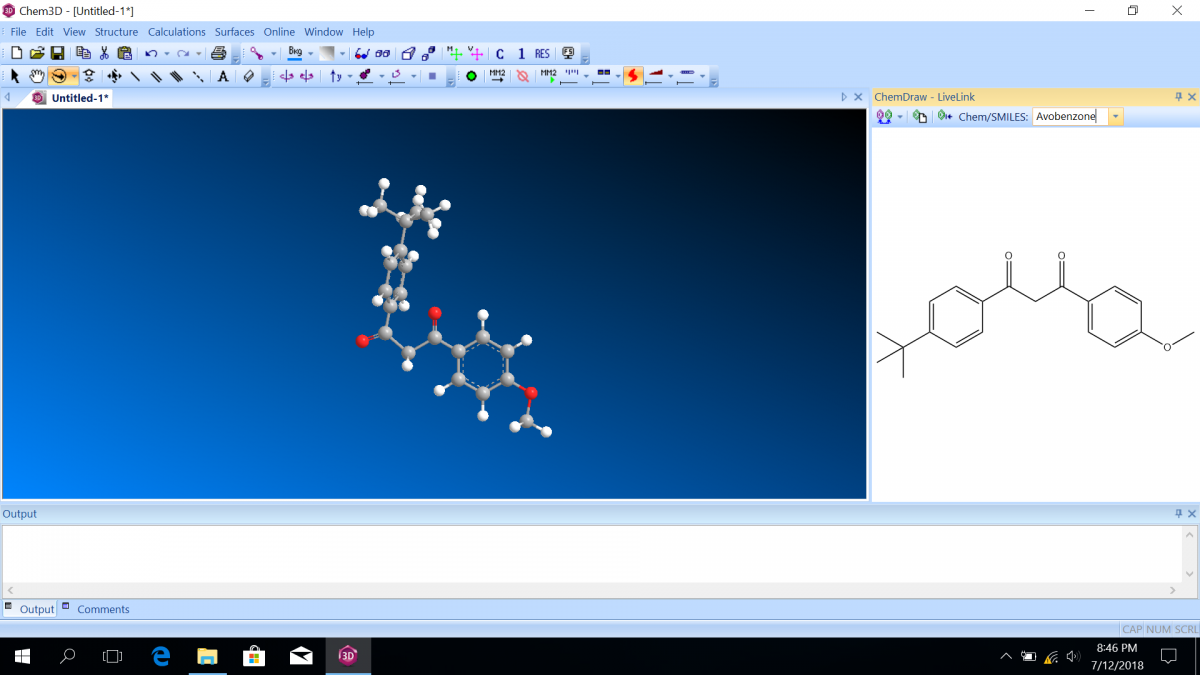
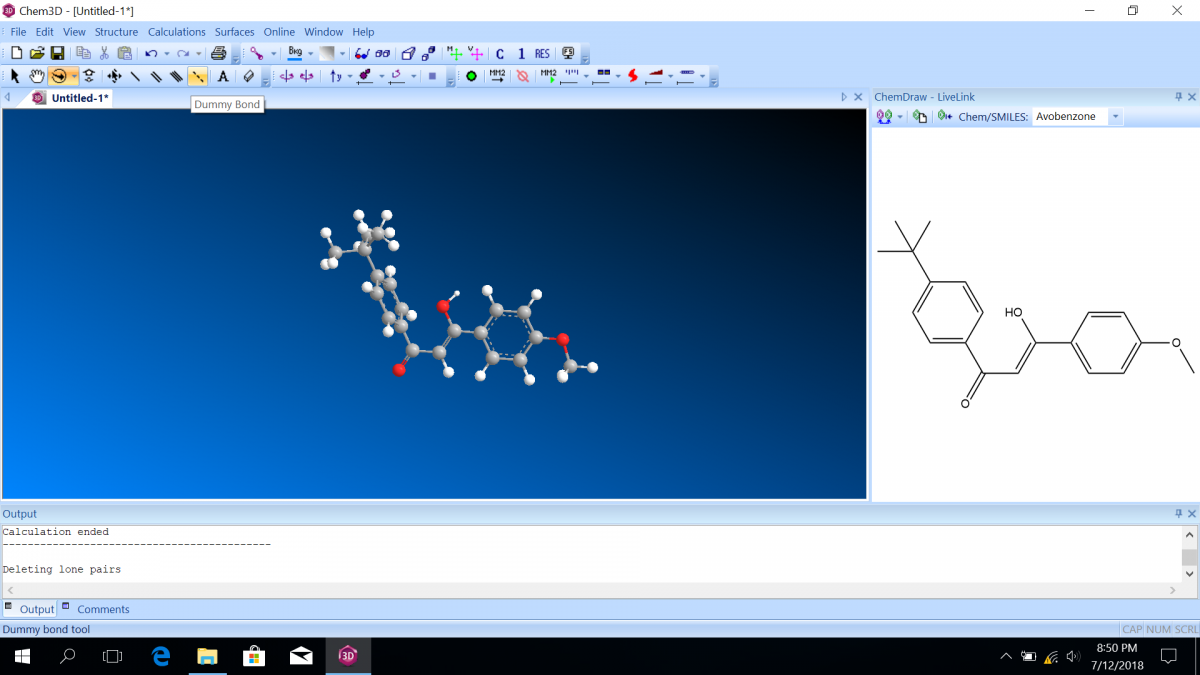
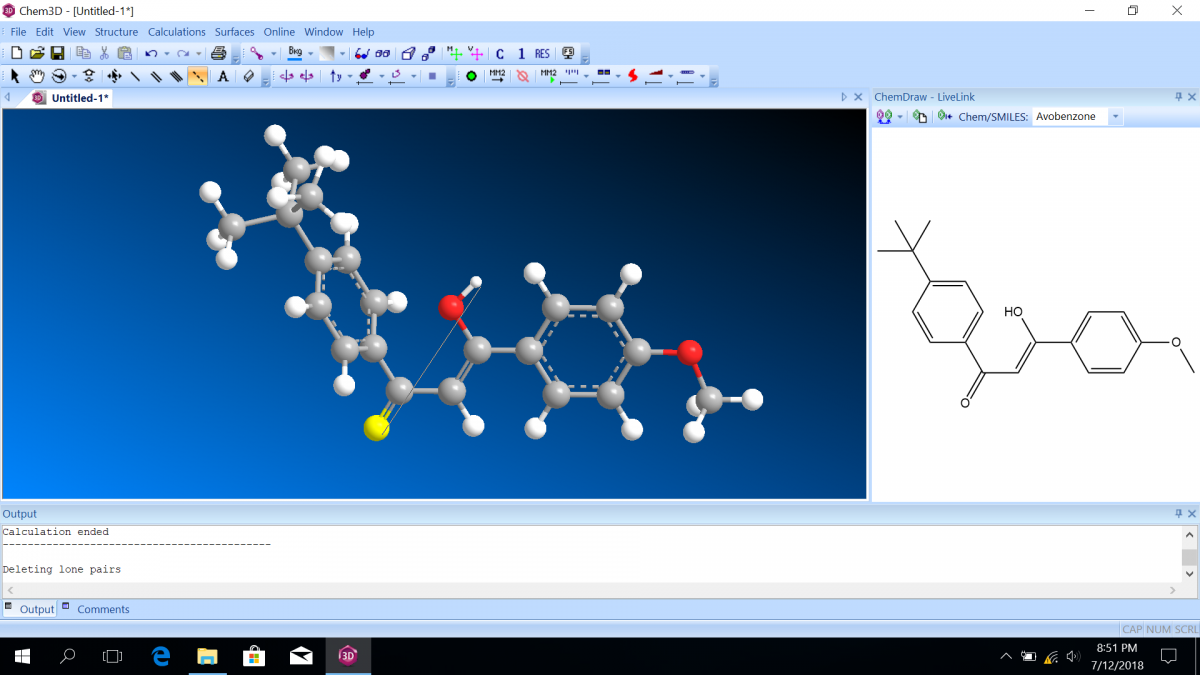
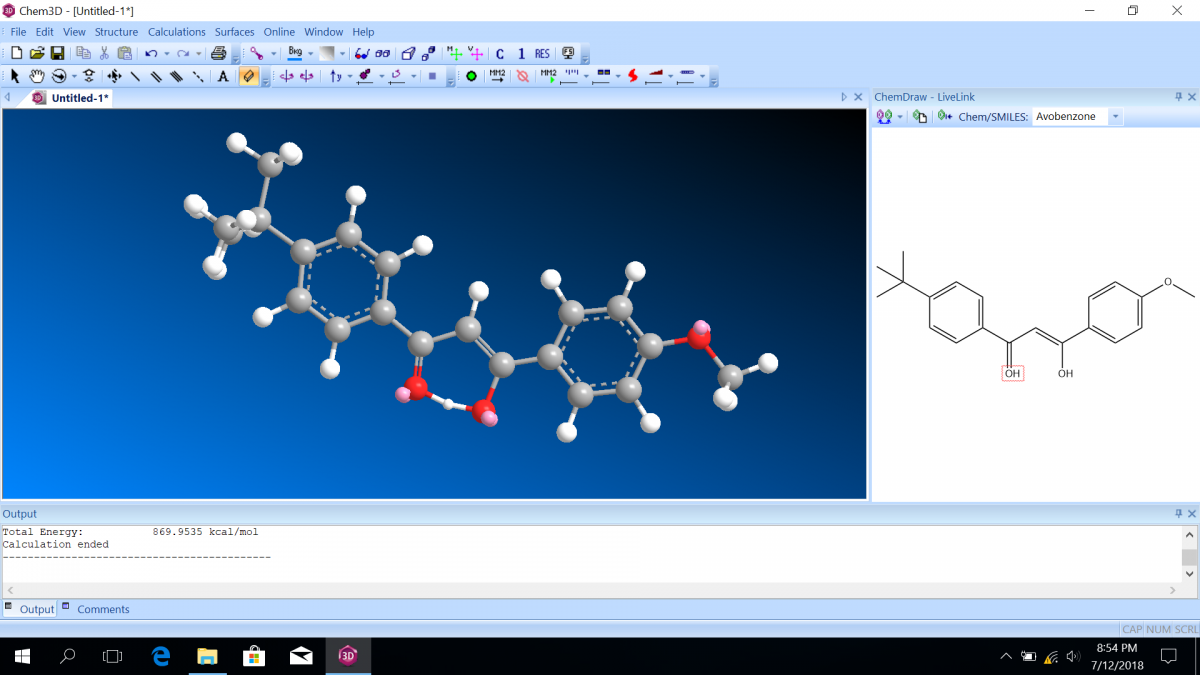
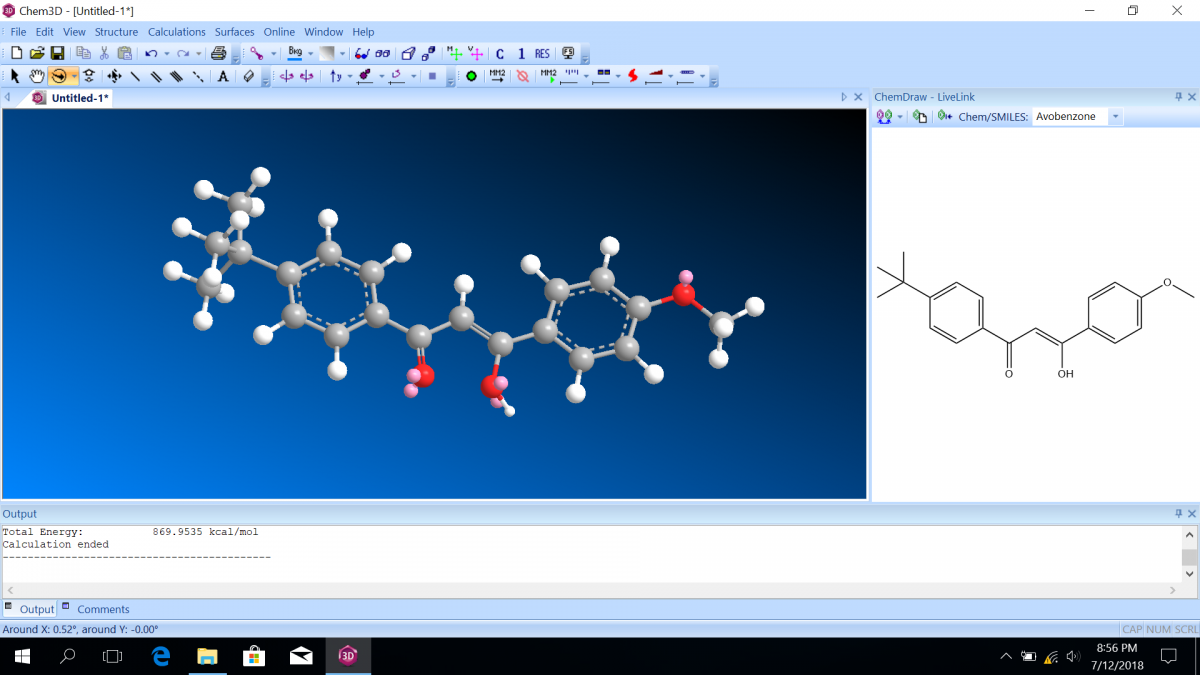
Most sunscreen products block UV light either by absorbing UV or reflecting UV. Mineral-based sunscreens such as titanium dioxide or zinc oxide mostly reflect UV, and organic molecules mostly absorb UV. In this lab, we are using a line of organic-based sunscreens that all have avobenzone as the primary active ingredient. Below is a line diagram of avobenzone. You can see that it exists in two isomer forms, which are called tautomers in this case. One tautomer absorbs UV-A (320 – 400 nm), and one absorbs UV-C (100 – 280 nm). Although the higher energy UV-C is very dangerous in theory, it is absorbed by just about everything, and as a result, unable to penetrate the skin. It is the lower energy UV-A that we need sunscreen to absorb.
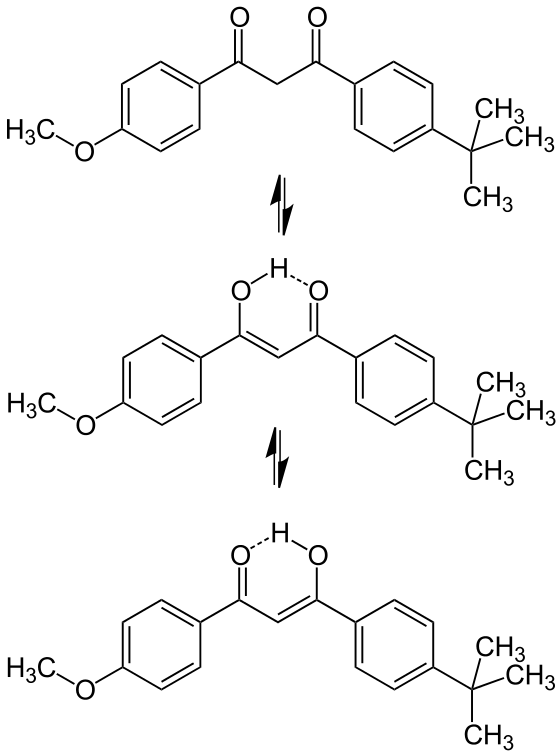
Avobenzone tautomeric forms. Top is the keto form, and middle and bottom are enol form. Note that the dashed line connecting the oxygen and hydrogen indicates hydrogen-bonding. Jü (https://commons.wikimedia.org/wiki/File:Avobenzone_Tautomeric_Forms_V1.svg), https://creativecommons.org/licenses/by-sa/4.0/legalcode
Avobenzone, like other organic molecules, can absorb a photon of light energy when an electron moves from a ground state, filled orbital to an excited state, unfilled orbital. The energy difference (ΔE) between the filled and unfilled orbitals is inversely related to the wavelength (λ) of light that can cause that transition.
ΔE = hc / λ
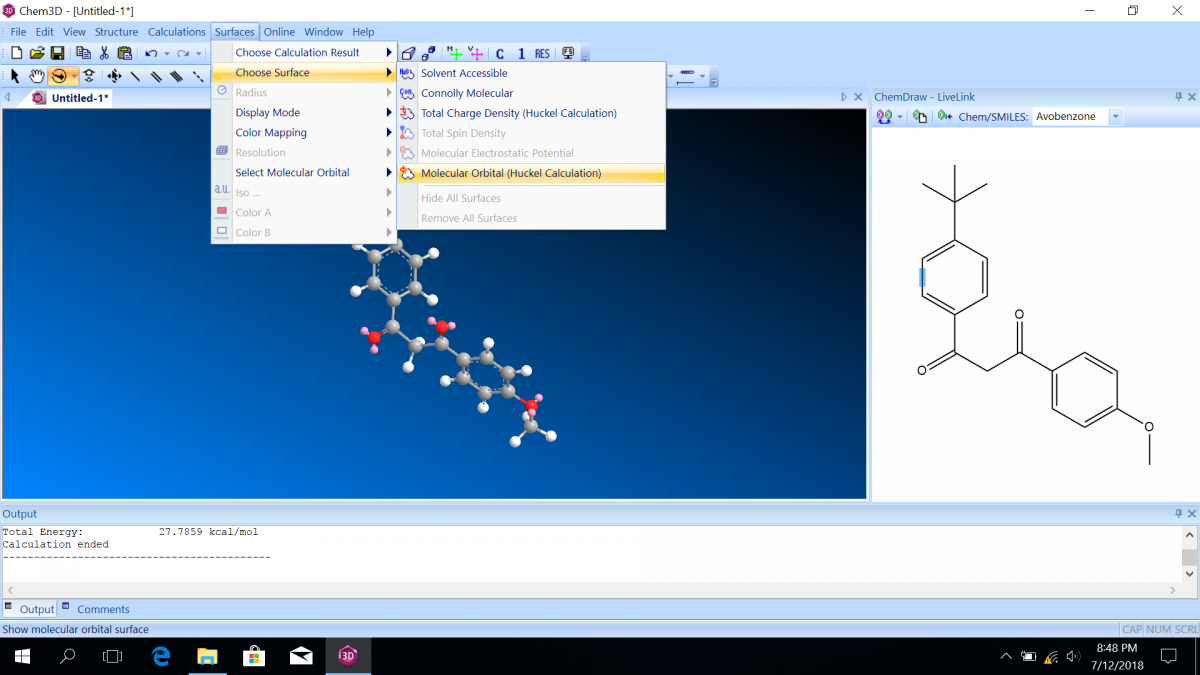
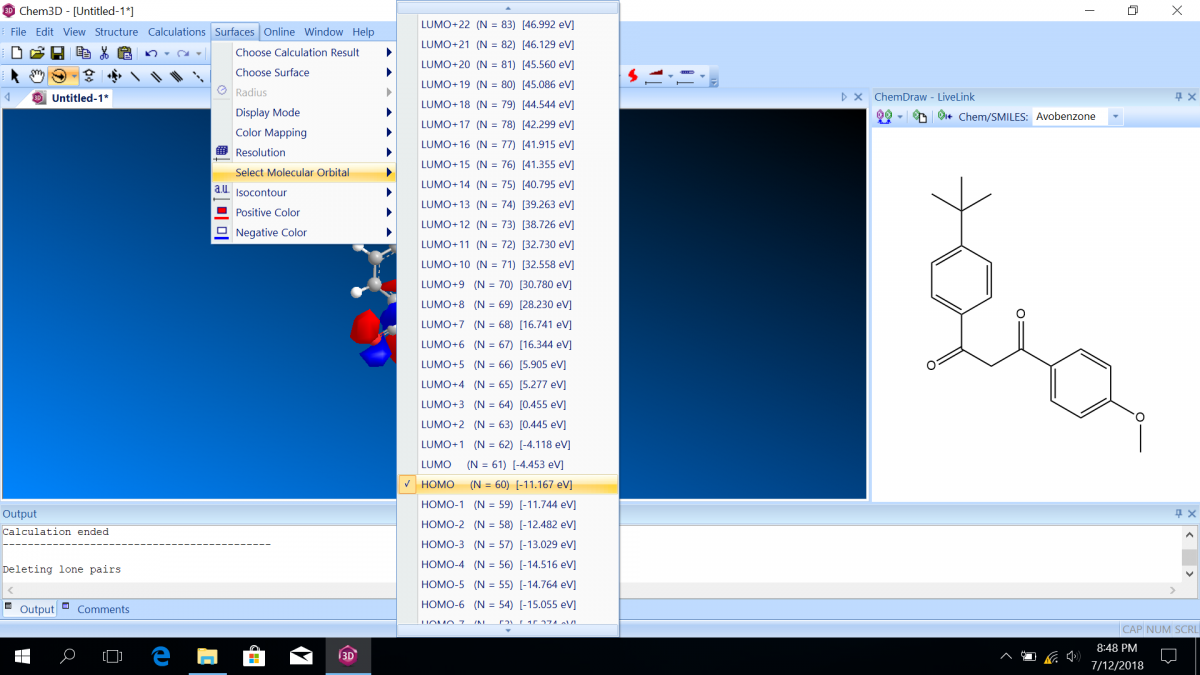
Molecular orbital diagrams predict the electron configuration in a molecule and can explain qualitative differences between molecules. In this lab, you will use molecular orbital theory to decide which tautomer of avobenzone absorbs UV-A and which absorbs UV-C. To verify your prediction, you will use Chem3D Pro molecular modeling software to calculate the wavelength of the absorptions. Note that these predictions are approximate and do not account for solvent effects.
Finally, you will measure the amount of light absorbed by the sunscreen samples at the wavelength that you calculate with the modeling software. A UV-Vis spectrometer will allow you to measure the amount of light absorbed at a given wavelength. Transmittance is a direct measurement of the fraction of the light that the sample blocks. (Note: transmittance doesn’t differentiate between a sample that blocks the light via absorption such as an organic sunscreen and a sample that blocks the light via reflection or scattering such as a mineral sunscreen. This is a source of uncertainty when making measurements on potentially scattering or reflecting samples).
Percent transmittance (% T) = Amount of light that passes through the sample / Amount of light applied to the sample x 100
You may expect percent transmittance to be proportional to the amount of sample present, but surprisingly, it is not. Consult with this webpage for a more complete explanation. Absorbance (A) is Log(1/%T), and this is proportional to the concentration of the chemical you are measuring. The Beer-Lambert law states:
A = ε b c,
where ε is a constant (“molar absorptivity”), b is the length of the sample where the light passes through, and c is the concentration of the sample. Since we are not measuring the concentration of the avobenzone, you will not need to use the Beer-Lambert law, but it may prove useful in future labs. Our spectrophotometers can measure either A or % T.
Note: perform this lab with a partner.
Follow the instructions on the lab worksheet to create hybridized molecular orbital diagrams for the bond between two carbons in each form of avobenzone.
Note: each group can have only 2 50-mL volumetric flasks. They will be used several times throughout this procedure. Be sure to rinse thoroughly between uses.
The first part of your data analysis will be normalizing the transmittance measurements according to the mass of the drop of sunscreen. The equation you will use to normalize the percent transmittance is somewhat complicated and unnecessary for you to derive on your own, but here are the details for those of you who are curious:
The exact amount of sunscreen that you used, the drop size, is directly proportional to the concentration (c) of sunscreen that you produce in the dilution procedure. According to the Beer-Lambert Law, the concentration of the absorbing chemical is directly proportional to the absorbance (A) of the chemical in solution. Absorbance is defined as Log(1/%T), where %T is the percent transmittance, so if you rearrange these expressions algebraically, then you see that %T is proportional to 1/10c. To normalize for concentration, you will divide your measured %T by 1/10c. This form is the most simplified form, which you should use to solve for Tables 4 and 5.
Normalized %T = measured %T × 10c
where c is the mass of the drop, which you recorded in Table 1.
Of course, the blank had no sunscreen, so you will not need to normalize its %T.
You will be making 2 graphs. Your graphs must all have titles, axis labels, axis units (if applicable), and a labeled legend. The legend should display the equation of the line of best fit and the R2 value. You can use Excel, Google Sheets, or any graphing software that you are comfortable with. I recommend Google Sheets if you are working very closely with a partner, but Excel is generally easier to use.
Fill out this worksheet. Turn in either a paper or digital copy.
Ideas for portions of this lab were drawn from the University of Pennsylvania Laboratory Program for Chem 53, accessed at this webpage: http://www.sas.upenn.edu/~kennethp/chemlab1.pdf, and the University of Calgary Laboratory Program for Organic Chemistry, accessed at this webpage: http://www.chem.ucalgary.ca/courses/351/laboratory/boilingpoint.pdf.

https://qph.ec.quoracdn.net/main-qimg-4161e9231033aa335aca697a3ef0c4e2
In many ways, chemistry can be a puzzle: since you cannot see atoms directly, you must instead collect as many pieces of data as you can and put them together to get the best possible answer. In this lab, you are tasked with identifying an unknown volatile liquid.
First, you will measure the molar mass of the liquid using the ideal gas law, but is the molar mass enough information to identify an unknown? How much uncertainty is associated with the molar mass measurement, anyway? If you were publishing a paper and wanted to convince the scientific community that you have identified a liquid, measuring the molar mass would surely not be enough information!
As additional pieces of evidence, you will measure the density in the liquid state, the boiling point, and the heat of combustion. These four pieces of evidence should pinpoint the exact identity of the liquid with enough certainty to convince even the most skeptical audience, who is hopefully yourself.
When you think you know the identity of the unknown, you can run a confirmatory test.
A volatile liquid is a liquid that vaporizes readily under normal conditions. Many volatile liquids have a noticeable smell because they vaporize into your nose! Throughout this lab, you will be working with a volatile liquid. When it is warm, it is mostly a gas, and when it is cool it is mostly a liquid. Note that you will be measuring the density of the substance in both the liquid and the gaseous state, but you will find that the tendency of the volatile liquid to vaporize and condense introduces uncertainty in both of these measurements.
The ideal gas law provides a way to relate the number of moles of a gas to the volume of the gas: n/V = P/RT
If you are also able to relate the number of grams of the gas to the volume of the gas (g/L, in other words, density), then these two formulas together allow you to then relate the number of grams of the gas and the moles of the gas, which is the molar mass: molar mass = (density)RT / P.
Your textbook shows a more detailed derivation in Section 8.3.
In this lab, you will measure the density of a volatile liquid in its gaseous state, the pressure, and the temperature, and this will allow you to calculate the molar mass. To measure the density, you will need to measure the mass and volume of a gas. The procedure will guide you through forming the gas and measuring the mass, but you must design your own method of measuring the volume of the gas. Be creative! Try to get as many significant figures as possible.
This is a topic you have not yet covered, but you will soon! Here is a simple explanation of what you need to know for this lab:
The heat of combustion is the amount of energy released when a given amount of a substance is burned in the presence of excess oxygen. Normally this value is reported in terms of energy per mole of the substance, but because we do not yet know the molar mass of the liquid, we will measure it in terms of energy per gram of the substance and compare it to the list of possible sample identities at the bottom of this page, also in those units, in order to identify the liquid.
You should be very comfortable measuring the density of a liquid. You just need the mass and the volume: density = mass/volume. You will be comparing the density of your liquid to the list of possible sample identities at the bottom of this page to help you identify the liquid.
Refer back to Lab 1 for a refresher on density measurements.
Boiling point is the temperature at which a substance changes from a liquid state to a gaseous state. Boiling point is actually a function of pressure, but because most people measure it under atmospheric pressure, it is typically reported at 1.000 atm (1013 mbar). If you notice that the atmospheric pressure on the day of your measurement is greater than or less than 1013 mbar, know that this will contribute to a discrepancy between your results and the literature boiling point values.
Note: do this lab with a partner. There are five parts to this lab, which will be done over two weeks. I suggest doing part 1 on the first week and parts 2-5 on the second week, although you may chose to do parts 2 and 3 whenever it is convenient. Be sure to use the same thermometer throughout the experiment.
At some point, you probably had this thought but were afraid to say it out loud: “are these thermometers right? I always thought water boiled at 100 °C, but it looks like this water is boiling at 105 °C. I don’t know, maybe I’m reading it wrong?” If you have had this thought, then pat yourself on the back for being observant. The alcohol thermometers are not perfect, and to get a reasonably accurate temperature measurement with them, you will need to calibrate them. Since we are making most of our temperature measurements in this experiment near 100 °C, we will calibrate at 100 °C.
Bring a beaker of tap water to a rolling boil over a bunsen burner. It doesn’t matter what size beaker and exactly how much water, but a 600 mL beaker about 3/4 filled with tap water would be a great choice. Once boiling, place your thermometer into the water. Hold it or clamp it so it doesn’t touch the bottom or sides. When the temperature is stable, record the “thermometer calibration temperature” to the nearest 0.2 °C in Table 1.
You can now calculate the offset for your individual thermometer.
100.0°C – “thermometer calibration temperature”(°C) = thermometer offset (°C)
This number may be positive or negative. Use a piece of label tape to label your thermometer with its thermometer offset. From now on, factor that offset into your temperature measurements before recording them in your data table. Keep that calculator handy!
As an example, let’s say your thermometer calibration temperature is 105.0 °C.
100.0°C – 105.0 °C = -5.0 °C
Now you know to subtract 5.0 °C from every temperature you measure throughout the experiment. If your thermometer reads 92.2 °C, then record 92.2 °C – 5.0 °C = 87.2 °C.
Record the barometric pressure of the atmosphere in Table 1. If you have reason to believe the pressure is changing throughout the experiment (maybe there is a hurricane outside?), check it before beginning every trial, but normally checking at the beginning of the experiment is sufficient.
Use the same 125-mL Erlenmeyer flask throughout this section. Dry the Erlenmeyer flask thoroughly. Measure the mass of the 125-mL Erlenmeyer flask with an Aluminum foil cover secured with a rubber band. Trim the Aluminum foil cover to right below the rubber band. Record the mass of the covered flask in Table 1. Make a tiny hole in the foil cover with a thumbtack.
Set up a hot water bath with a 600 mL beaker about 3/4 filled with tap water, similar to the one shown:
Bring the water to a boil over a blue bunsen flame.
While the water begins to heat, remove the foil cover and rubber band, place about 2 mL of the volatile liquid from the small bottle into the Erlenmeyer flask, then replace the foil cover and rubber band.
Turn off the flame. Submerge the covered Erlenmeyer flask up to its neck in the hot water, and use a clamp to attach it to the ring stand. Add more water if you need it to cover the flask up to the neck, but try not to get the aluminum foil wet.
Also, submerge a thermometer in the water, and use a clamp to attach it to the ring stand.
Monitor the temperature of the water to ensure it stays around 90 °C (don’t forget to factor in your calibration offset). Turn on the flame if the temperature drops below 80 °C. Maintaining this temperature, watch the vapor escape through the pinhole. Watch for the vapor to stop escaping through the pinhole and for visible condensation in the flask to disappear (tendrils dripping down the sides of the inside of the flask). This should take no more than 10 minutes. If you continue seeing condensation after the first 10 minutes, turn up the heat because your thermometer may be reading low. You can verify that the vapor has stopped escaping by holding a small watch glass over the pinhole and seeing that no condensation develops right above the pinhole. As soon as the vapor stops, record the temperature of the hot water bath to the nearest 0.2 °C in Table 1. Be sure to factor in the calibration offset!
Remove the Erlenmeyer flask from the hot water bath, but keep the cover on. Be sure all of the liquid has vaporized. If there is visible liquid, put it back into the hot water bath for a few minutes. Dry the outside of the flask completely. Then, measure the mass of the covered flask with the vapor inside (it may condense back to a liquid). If the mass is not stable, let it cool longer. Record the mass in Table 1. Expect a mass around 0.2 g. Consider re-doing the trial if your mass is much lower or higher.
Repeat this procedure two more times for a total of 3 trials. You may reuse your hot water bath. You must use the same 125-mL Erlenmeyer flask every time, but make sure you dump out the gas and any condensation before weighing the flask empty. If your aluminum foil gets wet, then you should use a new piece.
Measure the volume of your Erlenmeyer flask using your method, your partner’s method, or a combination of the two. If you need to measure the mass of the water in the flask, be sure to use a high capacity balance such as the CPA324s, which measures up to 320 g. Try not to spill water on the balances. Be sure to clean it up if you do. Record your data in Table 2.
When it is your turn to use the bomb calorimeter, begin by preparing your sample for analysis:
The experimental sample – this is a clean sample cup with 1.00 g of the volatile liquid inside. Record the exact mass of the volatile liquid in a tared sample cup in Table 3. Cover the sample cup with a piece of parafilm immediately after recording the mass of the sample to ensure none of the sample evaporates.
Your instructor or TA will walk you through measuring the heat of combustion for the sample. You will need the mass of the liquid in order to operate the bomb calorimeter. Record your results in Table 3.
Use a clean, dry 100 mL volumetric flask with a ground glass stopper for this experiment. How many significant figures do you get? Ask if you are not sure.
Measure the mass of the empty volumetric flask and stopper. Record the data in Table 4.
Fill the volumetric flask exactly to the point where the bottom of the meniscus is on the ground line with the volatile liquid from the bottle labeled “use for density of liquid experiment.” Cover the flask immediately to ensure none of the liquid escapes.
Measure the mass of the filled volumetric flask and stopper. Record the data in Table 4.
I will provide a demonstration apparatus for this rather complex set-up, but this is a description of how to build it:
Use the same thermometer that you previously calibrated. If you aren’t sure it is the same one, repeat the calibration procedure and record the offset. Gently push a thermometer through a split rubber stopper. Push the stopper up past the 100 °C mark so you can read temperatures below this mark.
Secure a 5 or 10 mm glass test tube to a thermometer with a rubber band. Be sure not to cover the temperature marks too much; temperatures below 30 °C are probably fine to cover. Make sure the bottom of the thermometer and bottom of the test tube are lined up together.
Use a bunsen clap attached to the rubber stopper to secure the thermometer/test tube apparatus to a ring stand.
Pour about 1 mL of the volatile liquid into the test tube. Drop a boiling chip in the test tube. Then, drop a capillary tube open end down into the test tube, as shown in the illustration. CAUTION! These volatile liquids are all flammable. Keep it away from open flames.
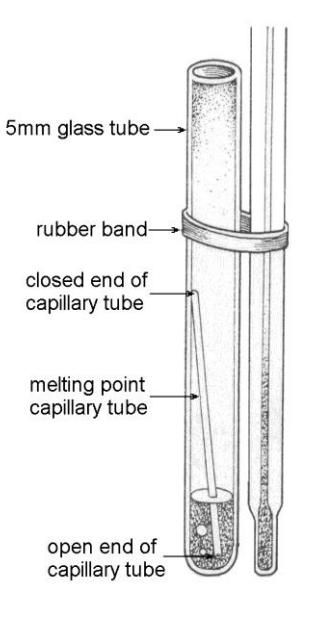
http://www.chem.ucalgary.ca/courses/351/laboratory/boilingpoint.pdf
Below this apparatus, you will need to make a hot water bath. Attach an iron ring to the ring stand about an inch above a bunsen burner, which is connected to the gas with amber tubing. Place a wire gauze on it. Place a 250 mL beaker filled 3/4 of the way with water on the gauze.
Lower the thermometer/test tube apparatus into the water bath, making sure to submerge the volatile liquid completely but allowing sufficient space above the water to ensure no water splashes into the test tube.
Turn on the gas and ignite the bunsen burner. Heat up the water nearly to boiling. Watch the test tube carefully. At first a few bubbles will come out of the capillary tube, but eventually you will see a steady stream of bubbles coming out of the capillary tube. When you see a slow, steady stream of bubbles, turn off the bunsen burner and allow it to cool. Your thermometer should read at least 85 °C before you turn off the flame (that temperature is above all of the possible boiling points). While it is cooling, watch the capillary tube. When you see it start to draw the volatile liquid up into the capillary tube, record the temperature as the boiling point. Be sure to record the temperature to the nearest 0.2 °C. You might miss it if you aren’t watching carefully the whole time it is cooling because it gets slurped up like a straw very quickly. IMPORTANT: be sure to factor in the offset that you found in Part 1 when recording the boiling point temperature. Record data in Table 5.
Repeat for 3 trials total. If three trials do not agree within 3 °C, consult your instructor or TA about performing additional trials. If necessary, refill the test tube and/or hot water bath between trials. Extinguish the flame before refilling or otherwise handling the volatile liquid.
Once you have completed your calculations and think you know the identity of the unknown, present your answer to the instructor or TA. She will provide a confirmatory test that you can use to validate your answer (or not!). Instructions for your test will be available at that time. Record the name of the test you used and the result. If the first test is negative, you may try a second test.
You can now calculate the molar mass of the unknown from the density of the gas. Then, compare the molar mass, the heat of combustion, the boiling point, and the density of the liquid state of the unknown to corresponding data from known substances. Use these results to select the identity of your unknown from this list of possible unknown liquids:
Fill out the worksheet for the report.

James Andrew Harris used separation chemistry to discover two new elements. http://www.cpnas.org/aahp/biographies/james-a-harris.html
James Andrew Harris was an American nuclear chemist who lived 1932 – 2000. While working at Lawrence Berkley National Laboratory (at the time, called Lawrence Radiation Laboratory), he helped discover synthetic elements 104 and 105, Rutherfordium and Dubnium. How are synthetic elements made? Often by smashing together very pure samples of lighter elements. Harris carefully produced these pure samples using separation chemistry.
These are a few more examples of the applications of separation chemistry today and in history:
In this lab, you will be separating a mixture of substances using physical and chemical separation techniques and deducing the original masses of each substance in the mixture.
The heterogeneous mixture you will begin with contains elemental iron filings, silicon dioxide (sand), sodium chloride, and sodium nitrate. You will be separating each of these substances using several common separation techniques that depend on the physical and chemical properties of the substances: magnetic separation, filtration, chemical coagulation, and finally evaporation.
Note: perform this lab with a partner.
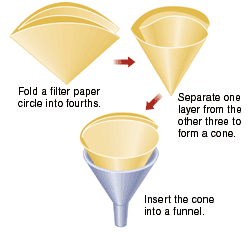
Filter apparatus https://alfa-img.com/show/filter-paper-and-funnel.html

The masses of the recovered iron filings and sand are directly measurable, but the masses of the salts require advanced stoichiometry to deduce. Embrace the challenge!
Fill out this worksheet. Turn in either a paper or digital copy.