Learning Goals

1. Practice using an analytical balance;
2. Practice using a graduated cylinder;
3. Apply significant figures rules to experimental calculations;
4. Perform linear regression.

Introduction

Dmitri Mendeleev

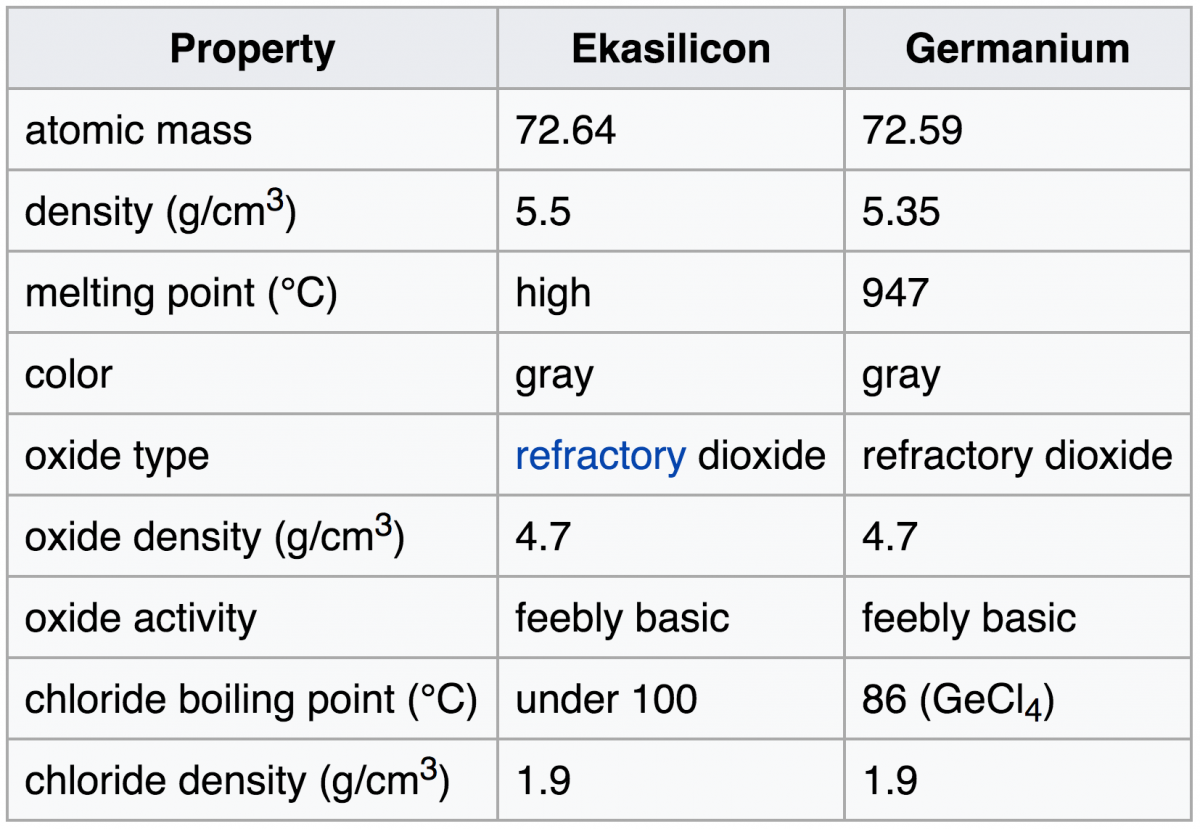
When Dmitri Mendeleev published the first periodic table, he arranged the elements to illustrate their periodic trends. Many elements that we know of today had not been discovered yet (Note: scientists continue to discover new elements today), so Mendeleev left gaps where there seemed to be discontinuities in the trends. One of these gaps was an element that seemed to be missing from group 14 between silicon and tin. He called the missing element “eka-silicon.”

Clemens Winkler discovered a new element in 1886. Its physical properties were similar to antimony and arsenic, but its chemical reactivity fit with elements in group 14, so it wasn’t clear where the new element fit on the periodic table. Finally, Winkler determined the atomic mass of the new element, which matched Mendeleev’s prediction for eka-silicon, so the element was placed in group 14 and named “Germanium” after his homeland of Germany.

https://en.wikipedia.org/wiki/Germanium

In this experiment, you will measure the density of 3 of the elements in group 14 and predict the density of Germanium.

Background

Density is defined as mass per volume. It is normally expressed in units of g/cm³ or g/mL (these are equivalent). Therefore, to measure the density of these elements, you will need to measure both the mass and the volume.

Measuring the mass is easy: we have highly accurate analytical balances. They are calibrated on a regular basis. Measuring the volume is a little trickier and requires careful attention to significant figures.

Procedure

Note: this lab is performed individually, but you will need to collaborate with two other students to complete the data analysis. Each student in your group of three will measure the density of one of the elements provided, and you will combine your results to predict the density of germanium. You may need to provide data for more than one group, depending on how many students are in your lab section.

Measurement of the density of a group 4 element

1. Obtain a sample of your element: For tin or silicon, use approximately 10 g. For lead, use approximately 25 g. Tare your weighing vessel. This could be a weigh boat or a small beaker. Place the sample in the vessel. Record the exact mass, including all of the decimal places displayed on the balance, in Table 2. Pro-tip: when you tare a weighing vessel, you are subtracting the mass of the weighing vessel from the mass of whatever you are weighing. Scientists normally use the balance to do this subtraction automatically by setting the mass of the empty weigh vessel to zero immediately before using the balance. 
2. Put approximately 15 mL of DI H2O (“deionized water”) into a 25-mL graduated cylinder. DI H2O is found in the small white faucets in every sink. Record the exact volume to the nearest 0.02 or 0.05 mL in Table 2. If you cylinder has graduation lines representing 0.2 mL, then estimate to 0.02 mL. If it has graduation lines representing 0.5 mL, then estimate to 0.05 mL. Ask your instructor or TA if you’re not sure how to figure this out.
3. Place the element sample carefully into the graduated cylinder. Make sure you don’t splash any water. Record the volume of the water and the sample to the nearest 0.02 or 0.05 mL in Table 2. Precision should match your previous measurement in step 2.
4. Dry the sample and return it.

Data analysis

1. Use your data from Table 2 to calculate the density of your sample. Record the density in Table 3.
2. Obtain the densities of the two other elements from two other students. Fill in  Table 3.
3. Use Excel or some other plotting software to plot the densities of each element as a function of period number on the periodic table (eg. Silicon would be 3, tin would be 5, etc.). If you are unfamiliar with plotting in Excel and linear regression, refer to the Excel lab techniques page or consult the CTLR. Here is an example of linear regression using Google Sheets.
4. Perform linear regression. Find the equation for a line that takes the period number and outputs a density for elements in group 14.
5. Input germanium’s period number (4) and solve for the predicted density of germanium.
6. Calculate the percent error for the predicted density of germanium compared to the literature density of germanium. Percent error is the absolute value difference between your experimental value and the literature value, divided by the literature value, multiplied by 100.

Report

Fill out this worksheet. Turn in either a paper or digital copy. Attach your graphs.