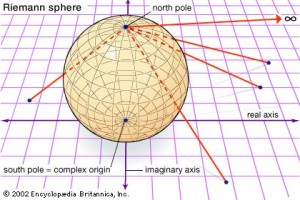
Other geometric contributions made by Riemann include a generalization of the metric of Pythagoras to complex spaces, and the Riemann sphere – both of which deal with the concepts of infinity. Riemann’s sphere is a step up from Bolzano’s principle which shows that there are the same number of infinitely many points between zero and one as there are between zero and two (reinforcing the concept that infinity is not a number but merely a concept). Riemann showed this using a Euclidian geometric and simple diagram (which is shown below).

http://media-3.web.britannica.com/eb-media/23/70823-004-2AD75C17.jpg

Riemann shows here that if we are to picture a sphere with a “north pole” point I will call “x”, lines can be drawn from , and down through the sphere to any other point “y”, which will emerge and intersect with a horizontal plane below that sphere. For each and every y, provided that y does not equal x, there will be an intersection on the plane. No matter the size of the plane, there can be a line drawn to hit a point on that plane. Essentially, this is showing how infinitely many points on the sphere can be mapped with the infinitely many points on the plane. However, point , represents the “infinity point”, as no line can go directly from it the plane without passing through the sphere. In fact, each and every line in any direction on the plane will go to this north pole, eliminating the concept of negative and positive infinity, and showing that all lines will converge at point . What’s more, each point on the plane can be compacted to the infinity point. Most people thought this was a revolutionary conclusion (if they had time to understand it).