One of the most important contributions that Aristotle had made to to study of infinity is identifying a dichotomy between what Aristotle calls the “potential infinite” and the “actual infinite”.

The potential infinite is a group of numbers or group of “things” that continues without terminating, going on or repeating itself over and over again with no recognizable ending point. What distinguishes the potential infinite and gives it the characteristic of being “potential” is the idea that if one were to take a sliver, or examine just one isolated portion of that infinite set of numbers, one would be able to capture or observe a finite set of numbers. The obvious example is the the grouping of natural numbers. No matter where you are while listing or counting out natural numbers, there always exists another number to proceed the one before. Also, a geometric line with a starting point could extend on without end, but could still be potentially infinite because all one would have to do is add on more length to a finite length to allow it to extend.

The actual infinite involves  never-ending sets or “things” within a space that has a beginning and end; it is a series that is technically “completed” but consists of an infinite number of members. According to Aristotle, actual infinities cannot exist because they are paradoxical. It is impossible to say that you can always “take another step” or “add another member” in a completed set with a beginning and end, unlike a potential infinite. It is ultimately Aristotle’s rejection of the actual infinite that allowed him to refute Zeno’s paradox.

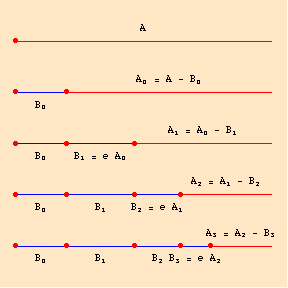
Although Aristotle did disprove the existence of the actual infinite finally, and tended to reject a lot of major concepts in  mathematics, the importance of mathematics was still never belittled in Aristotle’s eyes. Aristotle argued that actual infinity as it is not applicable to geometry and the UNIVERSAL, is not relevant to mathematics, making potential infinity all that actually is important.