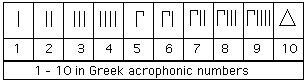
Aristotle could not accept one as a number as it could not simultaneously be the precursor to all other numbers within the number system and not possess a precursor for itself (0 having no value). One could only be sought after as a beginning (greek: archê), not an actual number. Aristotle’s conviction was that numbers must have plurality and wholeness; fractions could not be numbers. He viewed mathematics as an extremely physical study, relating all mathematical concepts with geometry, distance, and tangible objects (example: the Greeks often used pebbles to carry out mathematical calculations). He was a strong proponent of UNIVERSALITY in the same sense, often refusing to accept concepts of mathematics outside the real, physical world, and relying heavily on the idea that there exists one universal proof, justification, or explanation for any given problem.