Learning Goals
- Construct hybrid molecular orbital diagrams and connect this theory with properties of molecules;
- Perform computational chemistry calculations to form a theoretical basis for an experiment;
- Prepare solutions via serial dilutions;
- Explore limitations in measurements made with the spectrophotometer and analytical, including the differences between absorbance measurements and percent transmittance measurements;
Introduction
The sun emits a continuous spectrum of ultraviolet (UV), visible, and infrared light. Of particular concern is UV light, which the World Health Organization classifies ultraviolet (UV) light as a known carcinogen. This means that UV light causes cancer. UV light also causes erythema, commonly known as a sunburn, and damages skin fibers, evidenced by wrinkled and sagging skin. 
The Food and Drug Administration (FDA) regulates sunscreen products claiming to protect skin from the sun and assigns a numerical sun protection factor (SPF). The FDA currently requires in vivo testing to measure the SPF; this involves application of the sunscreen to a patch of a volunteer’s skin and then exposing the volunteer to a controlled UV light source until the skin develops a sunburn. The SPF is calculated by comparing the amount of time it takes to sunburn the skin with the sunscreen to the amount of time it takes to sunburn the skin without sunscreen. SPF 15 means it takes 15 times longer to burn the skin with sunscreen than the skin without sunscreen. Unfortunately, this testing requires that a human volunteer gets a sunburn, which increases their risk of skin cancer. The goal of this lab is to develop a laboratory-based scale to measure the SPF without harming human volunteers. Instead of measuring how well a sunscreen protects against sunburn in a human volunteer, you will measure how well a sunscreen blocks UV light in the laboratory using spectrophotometry.
Background
Most sunscreen products block UV light either by absorbing UV or reflecting UV. Mineral-based sunscreens such as titanium dioxide or zinc oxide mostly reflect UV, and organic molecules mostly absorb UV. In this lab, we are using a line of organic-based sunscreens that all have avobenzone as the primary active ingredient. Below is a line diagram of avobenzone. You can see that it exists in two isomer forms, which are called tautomers in this case. One tautomer absorbs UV-A (320 – 400 nm), and one absorbs UV-C (100 – 280 nm). Although the higher energy UV-C is very dangerous in theory, it is absorbed by just about everything, and as a result, unable to penetrate the skin. It is the lower energy UV-A that we need sunscreen to absorb.
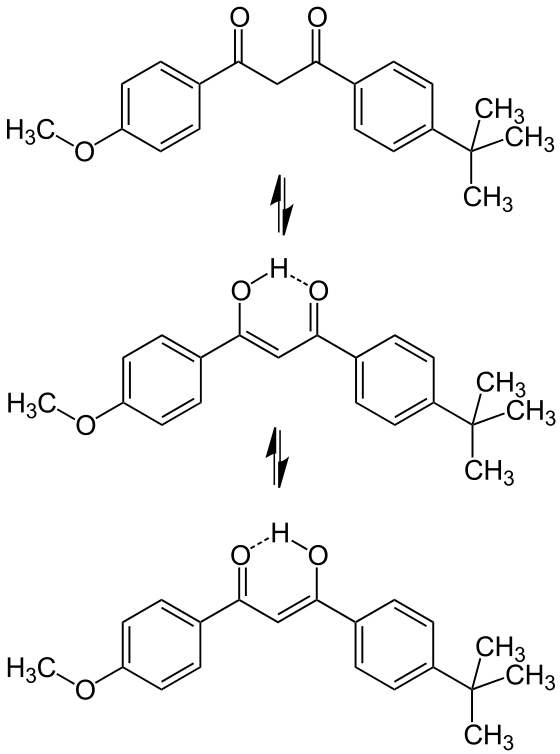
Avobenzone tautomeric forms. Top is the keto form, and middle and bottom are enol form. Note that the dashed line connecting the oxygen and hydrogen indicates hydrogen-bonding. Jü (https://commons.wikimedia.org/wiki/File:Avobenzone_Tautomeric_Forms_V1.svg), https://creativecommons.org/licenses/by-sa/4.0/legalcode
Avobenzone, like other organic molecules, can absorb a photon of light energy when an electron moves from a ground state, filled orbital to an excited state, unfilled orbital. The energy difference (ΔE) between the filled and unfilled orbitals is inversely related to the wavelength (λ) of light that can cause that transition.
ΔE = hc / λ
Molecular orbital diagrams predict the electron configuration in a molecule and can explain qualitative differences between molecules. In this lab, you will use molecular orbital theory to decide which tautomer of avobenzone absorbs UV-A and which absorbs UV-C. To verify your prediction, you will use Chem3D Pro molecular modeling software to calculate the wavelength of the absorptions. Note that these predictions are approximate and do not account for solvent effects.
Finally, you will measure the amount of light absorbed by the sunscreen samples at the wavelength that you calculate with the modeling software. A UV-Vis spectrometer will allow you to measure the amount of light absorbed at a given wavelength. Transmittance is a direct measurement of the fraction of the light that the sample blocks. (Note: transmittance doesn’t differentiate between a sample that blocks the light via absorption such as an organic sunscreen and a sample that blocks the light via reflection or scattering such as a mineral sunscreen. This is a source of uncertainty when making measurements on potentially scattering or reflecting samples).
Percent transmittance (% T) = Amount of light that passes through the sample / Amount of light applied to the sample x 100
You may expect percent transmittance to be proportional to the amount of sample present, but surprisingly, it is not. Consult with this webpage for a more complete explanation. Absorbance (A) is Log(1/%T), and this is proportional to the concentration of the chemical you are measuring. The Beer-Lambert law states:
A = ε b c,
where ε is a constant (“molar absorptivity”), b is the length of the sample where the light passes through, and c is the concentration of the sample. Since we are not measuring the concentration of the avobenzone, you will not need to use the Beer-Lambert law, but it may prove useful in future labs. Our spectrophotometers can measure either A or % T.
Procedure
Note: perform this lab with a partner.
Part I: Molecular Orbital Theory Prediction of Active Form of Avobenzone
Follow the instructions on the lab worksheet to create hybridized molecular orbital diagrams for the bond between two carbons in each form of avobenzone.
Part II: Molecular Modeling Calculation of the Peak Absorbance of Avobenzone
- Open Chem3D 15.1
- Click on the white panel to the right of the main window. It is titled “ChemDraw-LiveLink.”
- In the text bar, type “Avobenzone,” then hit “enter.” The keto form of avobenzone should appear.
- Optimize the structure by hitting “control-m.”
- There are several things you can do to get a better look at the molecule.
- You can click the third button from the left on the top toolbar to rotate the molecule. It looks like a circle with an arrow on it. After you click it, you can use the mouse to rotate the molecule.
- You can click “View” on the main menu, then click “Model Display.” This will present you with many options to change the display of the molecule. For example, “Display Mode” gives you more modes. The “Ball & Stick” mode is most common, but “Wire Frame” is convenient for a very complicated molecule, and “Space Filling” is helpful for visualizing atom size differences.
- After making the model and optimizing the structure, click “Surfaces” on the main menu, then “Choose Surface,” then “Molecular Orbital.”
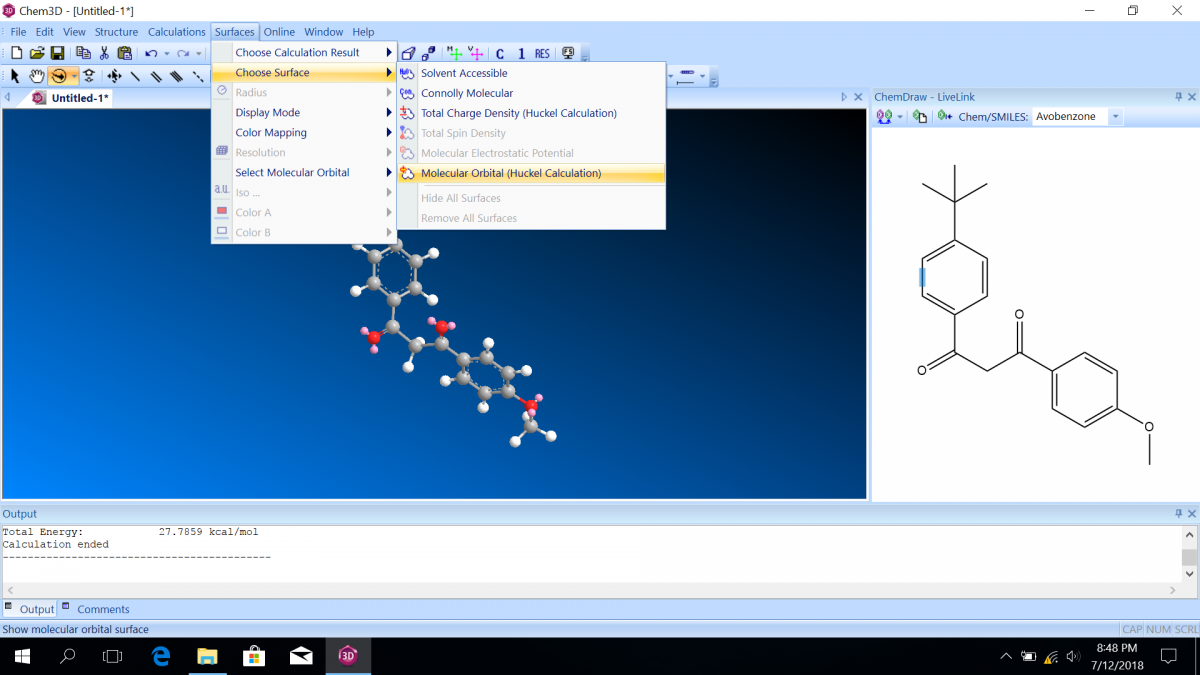
- The HOMO (highest occupied molecular orbital) will automatically be shown, but you can choose another molecular orbital from “Select Molecular Orbital.” You will also see the energies associated with each orbital. The labels are with respect to the HOMO and the LUMO (lowest unoccupied molecular orbital). Notice that the HOMO energy is usually negative, indicating a favorable state, but the LUMO energy is usually positive, indicating an unfavorable state (which is why it is UNOCCUPIED!)
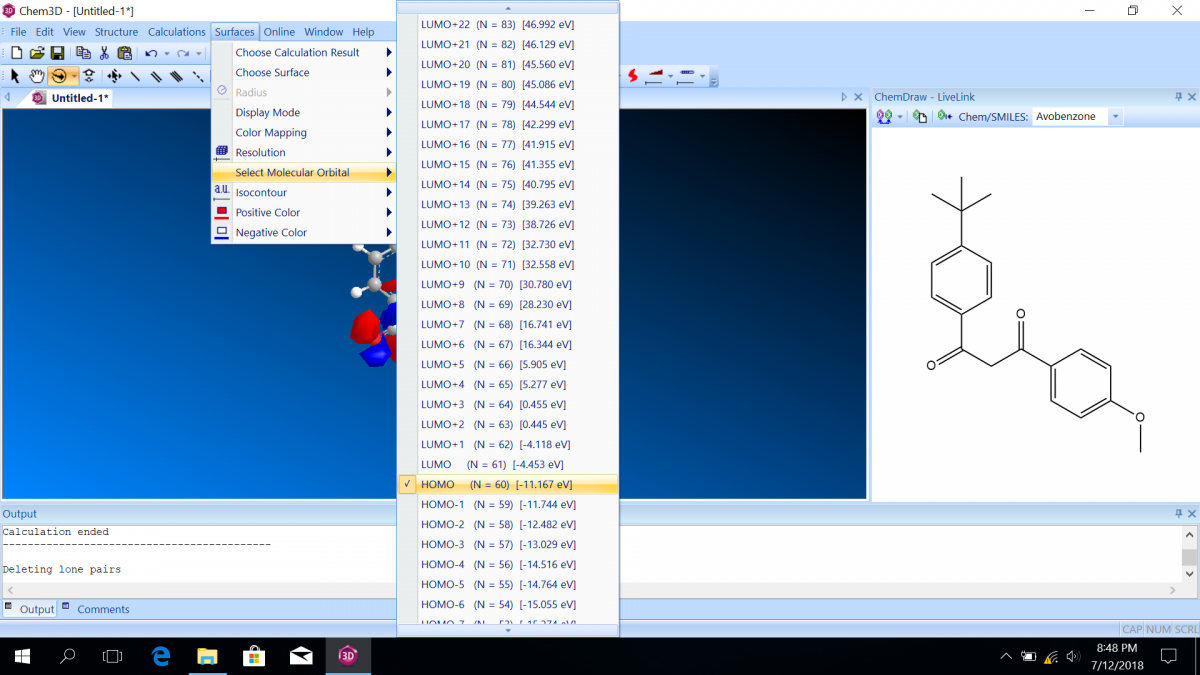
- The difference between the HOMO and the LUMO energies is the number you want to record; it usually corresponds to the strongest, lowest energy electronic absorption possible for the molecule. ChemDraw reports the the molecular orbital energies in terms of eV, so you will need to convert from those energy units to wavelength units in your post-lab.
- The HOMO (highest occupied molecular orbital) will automatically be shown, but you can choose another molecular orbital from “Select Molecular Orbital.” You will also see the energies associated with each orbital. The labels are with respect to the HOMO and the LUMO (lowest unoccupied molecular orbital). Notice that the HOMO energy is usually negative, indicating a favorable state, but the LUMO energy is usually positive, indicating an unfavorable state (which is why it is UNOCCUPIED!)
- You will have to switch from the keto form to the enol form manually. Use the tools associated with the “ChemDraw-LiveLink” panel to edit the molecule.
- You will need to add a bond between two carbons and delete a bond between a carbon and an oxygen. There are two possible configurations of the enol form, but it doesn’t much matter which one you make. The answers you get are almost exactly the same either way.
- The last step to form the enol is pretty tricky.
- You have to get a “dummy bond” and attach the double-bonded oxygen to the hydrogen that’s attached to the single-bonded oxygen.
- Then, optimize the energy via “control-m.”
- Then, delete that dummy bond before continuing with the procedure to find the HOMO-LUMO energy difference for the enol form (repeating step 6).
- You have to get a “dummy bond” and attach the double-bonded oxygen to the hydrogen that’s attached to the single-bonded oxygen.
Part III: Absorption Spectroscopy of Sunscreens
Note: each group can have only 2 50-mL volumetric flasks. They will be used several times throughout this procedure. Be sure to rinse thoroughly between uses.
Blank the spectrophotometer
- Prepare a blank cuvette: pour approximately 2 mL of propanol into a cuvette. Label the sample “blank”.
- Set the spectrophotometer to measure at 357 nm. This should be pretty close to the wavelength you calculated in the modeling section of this experiment (within +/-20 nm). Set the spectrophotometer to measure percent transmittance.
- Load the “blank” sample into the spectrophotometer in the slot marked “B.” Leave the blank in the B slot for the entire experiment. Hit “measure blank.” This should cause the percent transmittance measurement to say something very close to 100.0%. Ask your instructor or TA if it does not read something between 99.0 and 100.5%. Watch this number for a couple of minutes to ensure your spectrophotometer is giving you a stable reading. If the reading drifts outside of the 99.0 – 100.5% range during a 5 minute period, you will need to let the machine warm up some more. Record the %T measurement for the blank in Table 2.
Measure %T for SPF 4, 8, 15, and 30 Samples
- Working with one sunscreen solution at a time, transfer about 2 mL of the solution into a cuvette.
- Put the cuvette into the spectrometer and take the %T measurement immediately. Record the measurement in Table 2.
- Repeat steps 1 and 2 for each sunscreen sample (SPF 4, 8, 15, 30). If necessary, re-blank the instrument between samples.
- Also record the masses associated with each sample in Table 1. This information is written on the bottles or the blackboard.
Prepare the SPF 50 sample fresh so you can explore how the sunscreen degrades through light exposure
- Tare a 50 mL volumetric flask.
- Use a wooden dowel to transfer a small glob of sunscreen from the tube to the volumetric flask.
- Record the mass in Table 1. It should be around 0.0250 g. If it is too much, just use the dowel to scrape some out.
- Fill the flask up to the line with propanol, cap, and shake vigorously. Scrape down the sides of the flask and resume shaking if you need to.
- Use a 10 mL graduated cylinder to remove 10.00 mL of the solution. Pour the rest of the flask down the drain. Put the 10 mL back into the flask and then fill to the line with propanol. Again, cap and shake vigorously.
- Immediately begin making measurements with the Genesys 30.
SPF 50 measurements
- Blank the Genesys 30 spectrophotometer at 357 nm with a cuvette filled with approximately 2 mL of pure propanol.
- Take out the blank and put in the SPF 50 sample. Record the initial %T in Table 2.
- Continue taking percent transmittance reading every minute for 10 minutes, recording the data in Table 3. Also write the initial %T in Table 3.
Part IV: Data Analysis
Normalization of Transmittance Measurements to Account for Various Drop Sizes
The first part of your data analysis will be normalizing the transmittance measurements according to the mass of the drop of sunscreen. The equation you will use to normalize the percent transmittance is somewhat complicated and unnecessary for you to derive on your own, but here are the details for those of you who are curious:
The exact amount of sunscreen that you used, the drop size, is directly proportional to the concentration (c) of sunscreen that you produce in the dilution procedure. According to the Beer-Lambert Law, the concentration of the absorbing chemical is directly proportional to the absorbance (A) of the chemical in solution. Absorbance is defined as Log(1/%T), where %T is the percent transmittance, so if you rearrange these expressions algebraically, then you see that %T is proportional to 1/10c. To normalize for concentration, you will divide your measured %T by 1/10c. This form is the most simplified form, which you should use to solve for Tables 4 and 5.
Normalized %T = measured %T × 10c
where c is the mass of the drop, which you recorded in Table 1.
Of course, the blank had no sunscreen, so you will not need to normalize its %T.
Graphing Data and Linear Regression Fits
You will be making 2 graphs. Your graphs must all have titles, axis labels, axis units (if applicable), and a labeled legend. The legend should display the equation of the line of best fit and the R2 value. You can use Excel, Google Sheets, or any graphing software that you are comfortable with. I recommend Google Sheets if you are working very closely with a partner, but Excel is generally easier to use.
- Graph SPF vs the concentration-normalized initial percent transmittance (data in Table 4). Fit the data with a line.
- Graph time (in minutes) vs the concentration-normalized percent transmittance for SPF 50 (data in Table 5). Fit the data with a line.
Report
Fill out this worksheet. Turn in either a paper or digital copy.
